El artículo anterior (Ajedrez: la memoria de la inteligencia) exponía hasta donde había llegado la psicología cognitiva en su comprensión de los procesos mentales del jugador de ajedrez, gracias a las investigaciones de Adrian de Groot, H. A. Simon, Fernand Gobet y otros. Concluíamos que en su resultado final, tras más de un siglo desde que empezó la búsqueda de la “inteligencia ajedrecística”, ya no se hablaba de Inteligencia sino de Pericia, Expertise en lengua inglesa. Y en el importante debate sobre si existe algún beneficio educativo en proporcionar instrucción en ajedrez a edades tempranas, Gobet y Campitelli concluían que no se ha encontrado evidencia en ningún estudio, tal y como era de esperar sabiendo que las distintas pericias son menos reutilizables entre sí cuánto más especializados son sus ámbitos de aplicación. Y el ajedrez es una pericia muy especializada.
Pero Gobet y Campitelli abrían la puerta a una posibilidad teórica, la de una transferencia entre lo más general y compartido por todas las pericias: la transferencia de la inteligencia.
«Una visión diferente de la transferencia surge del estudio psicológico de la inteligencia. Los investigadores en este campo creen que una o unas pocas habilidades transferibles forman la base de la inteligencia. Estas habilidades se consideran generales, al menos dentro de los dominios verbales o visuoespaciales, y se supone que se aplican a una variedad de dominios (ver Sternberg, 2000, para una descripción general). Sin embargo, estas habilidades básicas también se consideran innatas y, por lo tanto, no susceptibles de mejora a través de la práctica. Finalmente, otros investigadores han propuesto recientemente que la mejor manera de entrenar habilidades transferibles es enseñar habilidades genéricas, como estrategias para aprender, métodos para resolver problemas y técnicas para razonar. Este enfoque ha logrado cierto éxito limitado (Grotzer & Perkins, 2000).» (Beneficios educativos de la instrucción en ajedrez, Gobet y Campitelli, 2006)
Parece como si la psicología cognitiva se mordiera la cola y, después de concluir que el ajedrez es «pericia», lanzara un guiño a las primeras y extraviadas investigaciones de Binet, Djakow, Petrowski y Rudik. Ha pasado más de un siglo desde entonces. Inteligencia sigue siendo una palabra de un obvio sentido para el común, pero no así para especialistas, filósofos, psicólogos y pedagogos, que a diferencia y semejanza de la Torre de Babel, parece que hablan la misma lengua pero con sentidos diferentes, como los teólogos bizantinos.
Gobet y Campitelli, en su trabajo “Beneficios educativos de la enseñanza del ajedrez: una revisión crítica”, concluyen: “En la mayoría de los estudios, no se utilizó ninguna teoría bien establecida para predecir resultados o justificar por qué el ajedrez debería ayudar”. Uno de esos estudios, la tesis de licenciatura presentada en 1976 por Johan Christiaen en la Universidad Nacional de Gante, Bélgica, se apoya explícitamente en la epistemología genética de Jean Piaget, y pretende medir y constatar esos presuntos beneficios de la instrucción ajedrecística a través de dos tests típicamente piagetianos: el test de la balanza y el test de los líquidos, que explicaremos en su momento.
La epistemología genética trata de la Inteligencia, ése es su objeto aunque ella misma no lo formule de una manera tan simplona. Por tanto, el estudio de Johan Christiaen trata de la transferencia de la inteligencia, no de una transferencia al buen tun-tún.
La epistemología genética.
Pero ¿qué es la epistemología genética? ¿Se trata de otra voz más en esa torre babeliana que han levantado los estudiosos de la Inteligencia? En absoluto. Se trata de una voz llena de sentido que destaca por encima de la confusión, y por eso me dio esperanzas tratar de conocer de primera mano ese estudio de Johan Christiaen de 1976.
Antes de entrar al detalle del trabajo de Johan Christiaen, será necesaria una breve presentación de la epistemología genética, que puede obviar cualquiera que la conozca.
La epistemología genética estudia los procesos por los cuales los seres vivos (genética) adquirimos conocimientos (epistemología), esquemas o pericias válidos para adaptarnos a nuestro entorno. Obsérvese que Epistemología es una rama de la Filosofía, pero que Genética es una rama de la Biología.
Históricamente la Filosofía, ecosistema extremadamente propicio para las discusiones bizantinas, ha oscilado pendularmente entre dos posturas extremas acerca de la posibilidad del Conocimiento: el apriorismo y el empirismo. Pido perdón al lector por haber resumido en una frase, y por lo tanto tergiversar y falsificar, más de dos mil años de sesudos debates. Seguramente en la mente del lector habrán resonado ecos escolares acerca de las Ideas (Platón), que están fuera de nosotros y entran en nosotros para poseernos, y su opuesto, las verdades inmanentes que surgen desde el interior de nuestro espíritu (Kant, por ejemplo). Le sonará la oposición entre Sujeto que conoce y Objeto conocido. Y preguntas como de dónde nace el conocimiento, del Objeto o del Sujeto, etc, etc.
Para la epistemología genética el sujeto del conocimiento es todo ser vivo. No solamente el sabio, el filósofo, el lógico, el matemático o el científico. Ni siquiera el ser humano, sino todo ser vivo es sujeto o protagonista del conocimiento. Los moluscos, por ejemplo. Y pongo este ejemplo chocante para traer a colación una pincelada biográfica de Jean Piaget, impulsor de la epistemología genética. De niño, era tal su empeño y curiosidad por la naturaleza y la biología que a los 14 años se le ofreció encargarse de la conservación de la sección de moluscos del Museo de Ciencias Naturales de Ginebra. Cargo que no pudo aceptar pues estaba en edad escolar y debía continuar con sus estudios. Se doctoró con una tesis en Malacología, tal y como era de esperar.
Para la epistemología genética el objeto del conocimiento es todo lo que interacciona con el sujeto: el entorno, la naturaleza, el medio y el propio sujeto. Y el conocimiento, ese lazo cognitivo entre sujeto y objeto, es el producto de la adaptación del ser vivo a su entorno. “Quien entienda al babuino hará más por la metafísica que Locke”, escribió Darwin. Y en cita de paralelo sentido del propio Piaget: «El niño explica al hombre tanto, y a menudo más, de lo que el hombre explica al niño.»

Una de las réplicas sísmicas del evolucionismo darwiniano fue la “evolución creativa” del filósofo francés judeocatólico Henry Bergson. Para Piaget, nacido en el seno de una familia intelectualmente muy rica con una madre profundamente religiosa, Bergson fue una influencia adolescente que le inspiró esa meta intelectual tan duradera y profunda que se suele adquirir a esa edad. Su meta no fue otra que la explicación biológica del conocimiento. Para Piaget, entre el problema filosófico del conocimiento y su explicación biológica, cual espada en nudo gordiano, había un eslabón pendiente de completar: la mente humana. Fue así que después de licenciarse con una tesis doctoral sobre moluscos, Piaget dio el salto a la psicología, aunque él no se consideró nunca tanto un psicólogo como un genetista.
En uno de sus trabajos de juventud, después de trasladarse a París para continuar estudios en la Sorbona, colaboró con Teophile Simon, coautor junto a Alfred Binet (¿les suena?) de los primeros tests de inteligencia. El doctor Simon encargó a Piaget la estandarización de unos tests de razonamiento diseñados por Cyril Burt e incorporados a los tests de Binet-Simon que se aplicaban en Francia. Esa tarea accidental, combinada con la formación naturalística de Piaget y sus hábitos de meticulosa observación, le llevó a indagar y a preocuparse más por los casos en los que los niños fracasaban en responder correctamente a las pruebas de razonamiento que por la distribución por edades de las respuestas correctas. Típicamente, detectó que algunas cuestiones lógicas básicas relacionadas con la teoría de conjuntos, no eran accesibles para los niños menores de 11 o 12 años.
Entiéndase el giro copernicano que da Piaget a las investigaciones de Binet y Simon: no le interesa saber qué porcentaje de niños a cada edad alcanzan la comprensión de determinados principios lógicos y en base a ello poder aplicar masivamente los tests de inteligencia para clasificar a esos mismos niños en más y menos retrasados y adelantados. Quería saber cómo razonaban los que fallaban la prueba y comprender el proceso por el cual seis meses, un año o dos después, en su proceso de maduración, esos mismos niños darían el salto cognitivo.
En palabras del propio Piaget, la inteligencia no es lo que se sabe, sino lo que se hace cuando no se sabe (L’intelligence ce n’est pas ce que l’on sait, mais ce que l’on fait quand on ne sait pas). La epistemología genética define la inteligencia como la capacidad de los seres vivos para mantener una constante adaptación de sus esquemas al entorno que los rodea.
El conocimiento, llamémosle “esquemas” en la terminología piagetiana o “pericia” en la terminología gobetiana, no es la inteligencia, sino su resultado, el resultado de la Adaptación, de la misma forma que el cuerpo y nuestro funcionamiento biológico se adaptan a condiciones cambiantes. La epistemología genética estudia los procesos por los cuales los seres vivos adquirimos conocimientos, esquemas o pericias válidos para adaptarnos a nuestro entorno.
Los procesos de Adaptación son básicamente dos: Asimilación y Acomodación.
La Asimilación es el proceso de incorporación en el ser vivo de todo lo que ocurre a su alrededor, siempre de acuerdo con los esquemas fisiológicos y mentales de que dispone en ese momento.
La Acomodación es el proceso por el cual el ser vivo modifica sus esquemas para reajustarlos mejor a su entorno, impulsado por una rotura del equilibrio existente anteriormente: o bien porque el entorno del sujeto ha cambiado y plantea diferentes o mayores exigencias, o bien porque la conducta exploratoria del sujeto le lleva a forjar un nuevo equilibrio, con nuevos y mejores esquemas.
Todo esto, explicado de manera tan sucinta, puede parecer mera palabrería si se desconoce hasta qué punto la epistemología genética ha detallado mes a mes y año a año, con un número abrumador de observaciones concretas minuciosamente registradas, el maravilloso viaje de la inteligencia en el ser humano desde su nacimiento hasta la plenitud. Un cuaderno de bitácora con etapas y subetapas nítidamente diferenciadas, que reflejan la evolución de los esquemas mentales desde los primeros reflejos neonatales hasta la inteligencia formal operacional. Una evolución que no es lineal, que registra periodos de estabilidad y momentos de crisis, en la cual los nuevos esquemas no surgen de la nada, sino que son evolución de los viejos, que nunca desaparecen, siguen ahí como parte del sujeto. Resulta maravilloso que se pueda seguir hacia atrás la trazabilidad de los principios de lógica formal, geometría, aritmética y teoría de conjuntos desde la mente adolescente hasta los primeros balbuceos motores y sensoriales del bebé.
Por eso nos interesa el primer intento, y único que conozco, en tratar el ajedrez a la luz de la epistemología genética.
Johan Christiaen, 1976, Gante (Bélgica)
En 1976 Johan Christiaen presentó en la Universidad Nacional de Gante su tesis de licenciatura titulada Ajedrez y Desarrollo Cognitivo. La copia que ha llegado a mis manos es una traducción al inglés desde el original en lengua flamenca, hecha en 1981 por H. Lyman, por encargo de la Massachusetss Chess Association y la American Chess Foundation, entidades comprometidas en aquellos años en la defensa de las virtudes educativas del ajedrez.
El estudio consistió en dar instrucción ajedrecística a 20 niños de aproximadamente 11 años de edad durante 42 semanas repartidas a lo largo de dos cursos escolares, y al final de ese periodo comparar sus resultados en dos tests piagetianos, el test de la balanza y el test de los líquidos, con otro grupo de 20 niños del mismo entorno que no habían recibido instrucción ajedrecística.
En el estudio de Johan Christiaen, la instrucción de ajedrez impartida se apoya en un conocido y probado método de la época, Jeugd Schaak (Ajedrez para Jóvenes) por B. Withuis. de amplia difusión en Holanda y la parte flamenca de Bélgica (Flandes). El método comienza obviamente enseñando los movimientos de las piezas, pero abarca todos los conocimientos, consejos y nociones necesarios para que los niños puedan jugar partidas de competición en condiciones de torneo. De hecho, al final de su instrucción los sujetos del estudio compitieron en un torneo escolar a nivel de Bélgica, con buen resultado, así como en otro torneo en el ámbito de su escuela, además de los juegos desarrollados en clase.
Los resultados del estudio no respondieron a las expectativas. En la resolución del test de la balanza y del test de los líquidos, tan sólo se pudo apreciar una leve mejora en el grupo de 20 niños “ajedrecistas” frente al grupo de niños que no habían recibido instrucción en ajedrez. Una mejora tan leve que el rigor estadístico del propio Johan Christiaen le lleva a calificar de no significativa.
Lo que llama la atención de este trabajo no es su falta de conclusiones. Es decir, que no se encontrara evidencia de que ninguno de los dos grupos se desempeñara significativamente peor o mejor en el resultado de los tests. Llama la atención el enfoque del estudio, que a diferencia de todos o la mayoría de los demás analizados por Gobet y Campitelli, al menos contenía una suposición concreta (aunque equivocada, como veremos más adelante) de lo que era común a la actividad cognitiva “jugar al ajedrez” con la actividad cognitiva que se pretendía medir como resultado, los dos tests piagetianos.
Porque no se entiende que se trate de conectar el ajedrez con presuntos beneficios en la comprensión lectora o en las matemáticas o en cualquier otra área de conocimiento, sin tener al menos una hipótesis fundada que relacione el ajedrez con esos contenidos educativos. Más allá de ese tópico de que “el ajedrez es un juego de inteligencia, luego el ajedrez debe ser bueno”, esos estudios carecen de otro fundamento que no sea el de una apariencia de rigor cuantitativo estadístico que impresiona a los legos, pero que expertos como Gobet y Campitelli se encargan de desmontar. Aún así, aún cuando esos estudios fueran impecables en sus técnicas estadísticas, nada puede reemplazar en el conocimiento algo tan básico como la comprensión cualitativa de lo que estudias. La cuantificación estadística no es más que una derivada sofisticada de algo tan simple como es la repetición: la repetición, para el ser vivo cognoscente, es una llamada de atención. En mi perro, es una pauta que le invita a la anticipación, que es su forma de conocer, de adaptarse al mundo. En el ser humano adulto la repetición, y también su ausencia inesperada, es una llamada de atención, una incitación a la explicación, la inferencia, la causalidad… Podremos medirla de la manera más sofisticada que se nos ocurra, pero nunca podremos prescindir de comprenderla.
En sus conclusiones sobre los siete estudios analizados, Gobet y Campitelli decían:
«En la mayoría de los estudios, no se utilizó ninguna teoría bien establecida para predecir resultados o justificar por qué el ajedrez debería ayudar; creemos que esto debilita el caso de la enseñanza del ajedrez, principalmente porque la posición predeterminada de la mayoría de los psicólogos y pedagogos es que la transferencia [de habilidades cognitivas entre un dominio y otro] es poco probable. Por lo general, se utilizan teorías de «sentido común», un enfoque bastante débil. Por ejemplo, Frank (1981, p. 72), en un estudio reportado objetivamente, concluye que “la destreza en el juego de ajedrez requiere la posesión de un gran número de aptitudes en mayor o menor grado, pero todas ellas necesarias”. Esta afirmación se usa a menudo en la literatura como apoyo para la educación en ajedrez. Sin embargo, en su forma débil, esta es una declaración vacía, en el sentido de que es probable que la mayoría de las actividades humanas aprovechen múltiples habilidades (p. ej., matemáticas, deportes, música) y, en su forma fuerte, es empíricamente incorrecta (p. ej., los resultados de Djakow et al., 1927, o incluso los propios datos de Frank, donde varias habilidades no se correlacionaron con la habilidad ajedrecística). De manera similar, Margulies (sin fecha) explica su resultado de que los puntajes de lectura se ven afectada positivamente por la enseñanza del ajedrez de la siguiente manera: “Los ajedrecistas combinan procesos de alto nivel —conocimiento e información sobre la posición— y un enfoque interactivo en el que se considera cada ‘movimiento candidato’. muy parecido a una palabra o frase en la lectura. Los procesos de cognición son muy similares. Tanto el ajedrez como la lectura son actividades de toma de decisiones, y se puede esperar cierta transferencia de entrenamiento de una a otra (p. 11)”. Una vez más, el vínculo es, en el mejor de los casos, sugerente, y la mayoría de las actividades humanas (¡incluso ver una película!) involucrarían procesos similares.»
El estudio de Johan Christiaen se apoya en una teoría muy concreta y bien establecida: la epistemología genética. Otra cosa es que Johan Christiaen no haya interpretado correctamente el ajedrez desde el punto de vista de la epistemología genética y lo que ésta puede aportar al problema esencial de la transferencia, tal como lo resumíamos en el artículo anterior sobre la pericia ajedrecística, y en especial a su tercer supuesto: transferencia no de conocimientos, no de pericias, sino de inteligencia.
Los dos tests “piagetianos”.
El estudio de Johan Christiaen utiliza dos pruebas típicas de la epistemología genética para medir el desarrollo intelectual al final del periodo de instrucción ajedrecística: el test de la balanza y el test de los líquidos. Aunque aquí, por abreviar, los hemos llamado “piagetianos”, en realidad fueron muchas las personas que han colaborado en la definición, refinado y prueba de estos y otros muchos tests. Singularmente, la investigadora Barber Inhelder, cuyo libro “De la lógica del niño a la lógica del adolescente. Ensayo sobre la construcción de las estructuras operatorias formales”, en coautoría con Jean Piaget, puede dar una idea de la profundidad y riqueza de estas pruebas. El lector puede echarle una ojeada en este enlace, aunque solo sea al índice.
El test de los líquidos presenta al niño-adolescente cuatro frascos similares conteniendo líquidos incoloros e inodoros que parecen iguales, pero de muy diferente composición química: (1) ácido sulfúrico diluido, (2) agua, (3) agua oxigenada, (4) tiosulfato. A su lado, una botella de yoduro de potasio equipada con un dispensador cuentagotas (g) que contiene yoduro de potasio.
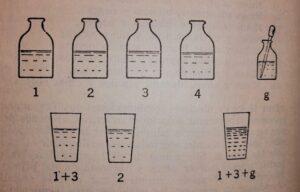
El niño-adolescente (o los niños-adolescentes, si la prueba se hace en grupo) desconocen el contenido de los frascos, por supuesto, así como sus propiedades cuando se combinan entre sí y con el yoduro de potasio: una mezcla de (1) ácido sulfúrico y (3) agua oxigenada se volverá de color amarillo al agregársele unas gotas de (g) yoduro de potasio, en tanto que el resto de combinaciones de un elemento o dos elementos permanecerán incoloras al recibir las gotas del reactivo. En cambio el tiosulfato (4) tiene la propiedad de decolorar la combinación amarilla 1+3+g.
Para despertar su curiosidad, los investigadores presentan dos vasos conteniendo líquido incoloro. Delante de los niños, agregan a cada vaso unas gotas de (g) yoduro de potasio. El líquido de uno de los vasos se vuelve amarillo (es decir, contiene 1+3 o quizás 1+2+3), en tanto que el otro permanece incoloro.
Se les pide a los niños que hagan “jarabe” (líquido amarillo) mediante cualquier combinación que consideren oportuna de los 4 líquidos y el reactivo (g). Se les proporcionan vasos en abundancia para poder realizar cuantas pruebas quisieran, así como papel y lápiz por si querían registrar los resultados.
El test de la balanza utiliza una balanza y un cierto número de pesas variables que pueden colocarse en los brazos de la balanza a distancias diferentes respecto de su centro, eje o fulcro. La balanza se presenta a los niños con dos pesos iguales situados a distancias desiguales del centro, por lo que la balanza está desequilibrada (la ilustración no es fiel reflejando este desequilibrio)
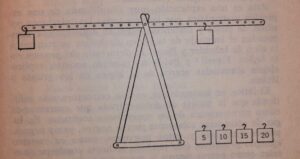
Se pide a los niños que equilibren la balanza.
Ambas pruebas, a distintas edades, provocan intentos muy significativos y reveladores de los esquemas cognoscitivos de cada niño en cada momento de su desarrollo. Por ejemplo, en el test de la balanza los niños más pequeños suelen presionar hacia abajo el brazo levantado, como una extensión de su propia experiencia sensorio-motriz y evidenciando que están todavía en el estadio preoperatorio (es decir, el estadio previo a las operaciones mentales en la terminología piagetiana).
¿Qué se pretende con estas pruebas? Averiguar si el niño-adolescente es capaz de una estrategia hipotético-deductiva que le permita llegar al conocimiento bien de las condiciones de equilibrio de la balanza, bien de las combinaciones de líquidos que satisfacen y no satisfacen la propiedad de “jarabe” (color amarillo)
Esa estrategia sólo es posible si el niño es capaz ya no solo de operaciones mentales concretas, sino de operaciones formales. Operación concreta versus operación formal es una importante distinción piagetiana. En el periodo previo (7-11 años aprox.) el niño es capaz de operar mentalmente, pero solo de manera concreta. No es capaz todavía de incluir en sus operaciones mentales aquellas que no son reales o actuales, sino sólo hipotéticas. Y por tanto, no es capaz de diseñar una investigación sistemática que le resuelva el problema del equilibrio de la balanza o de la combinación de líquidos que produce jarabe amarillo. Lo que no excluye que en algunas de sus pruebas al buen tun-tún consiga equilibrar la balanza u obtener jarabe, pero sin ser por ello capaz de explicarlo y reproducirlo. De la misma forma, enfrentado a una posición de ajedrez, se centrará en lo más evidente, el último movimiento del contrario y las amenazas directas que crea, y no tendrá en cuenta todas las posibles transformaciones del tablero. Su capacidad de cálculo es limitada porque no está des-centrada de los estímulos inmediatos.
Lo normal es que el adolescente alcance de lleno el periodo de las operaciones formales hacia los 13-14 años, siendo el periodo entre los 11 y los 13 años una fase de desequilibrio y transición, en la que la “inteligencia” innata pugna por “acomodar” en nuevos esquemas las realidades percibidas. En este sentido, el trabajo de investigación de Johan Christiaen ha elegido el momento óptimo en el que podría constatarse el beneficio de la instrucción en ajedrez en el desarrollo del pensamiento hipotético-deductivo. Haberlo planteado a una edad más temprana hubiera sido prematuro para una mayoría de chicos. Por cierto, se excluyó a las niñas del estudio por no saber «cómo enseñar ajedrez a las niñas». (With respect to sex, preference was given to boys, as less experience was available in giving chess instruction to girls, pag. 24)
Hemos definido el pensamiento hipotético deductivo como aquel capaz de incluir en sus operaciones mentales no solo aquellas que son reales o actuales, sino también las hipotéticas. Es en este sentido en el que el estudio de Johan Chrisitiaen compara toda actividad mental cognoscitiva, verse sobre lo que verse, balanzas, líquidos o ajedrez. Pero en este sentido nos surge un primer reparo: ¿son comparables entre sí las operaciones mentales que resuelven un problema de ajedrez, con las que resuelven el problema de la balanza o el problema de los líquidos? Veamos de qué naturaleza son las operaciones involucradas en cada problema.
En la resolución exitosa del problema de los líquidos, los niños toman en consideración todas las combinaciones posibles de n x n, con g como constante u operador que nos da el resultado, lo que hace 15 combinaciones sin contar la nula (ningún líquido de ningún frasco). De esta forma, se llega a la conclusión exacta de que todas las combinaciones con g en la que están presentes los líquidos 1 y 3, producen jarabe amarillo (1+3 y 1+2+3), salvo la 1+2+3+4, por la acción decolorante del tiosulfato (4). En términos de lógica formal, el niño ha utilizado el esquema del látice: para un grupo de cuatro proposiciones (los cuatro líquidos, por ejemplo) todas las combinaciones posibles de verdad-falsedad de esas cuatro proposiciones. Por ejemplo, 1+3 se expresaría lógicamente como «1 presente, 2 ausente, 3 presente, 4 ausente». Obviamente, el niño no tiene por qué saber lo que es un látice para someter a prueba todas las hipótesis posibles, como no tiene por qué saber gramática para hablar de manera gramaticalmente correcta.
El problema de la balanza también lleva a una toma en consideración de las combinaciones de pesos y distancias. No obstante aquí la estrategia de comprobar todas las operaciones posibles, mucho más numerosas que en el caso del test de los líquidos, sólo resultan exitosas cuando el niño o adolescente descubre la relación inversa entre el peso y la distancia. Una comprensión cualitativa que, a partir de este momento, dirige las pruebas para establecer las distintas formas de equilibración cuantitativa sumando/restando pesos, o acortando/alargando las distancias.
Estas formas de equilibración son comunes a otros problemas físicos (por ejemplo, vasos comunicantes) y tiene su expresión lógica formal en el grupo de operaciones INRC: Identidad (añadir un peso), Negación (quitar un peso), Reciprocidad (peso igual a distancia igual) y Correlación (peso mayor/menor a distancia menor/mayor>). De nuevo hay que recalcar que el niño no tiene por qué saber lo que es un grupo INRC, aunque utilice sus operaciones en la comprensión de los estados de equilibrio de distintos fenómenos físicos o no físicos.
¿Qué correlación puede haber entre los tres problemas -ajedrez, balanza y líquidos- más allá del hecho de que involucren la capacidad de operar mentalmente con hipótesis? Es perfectamente posible que un niño a una edad concreta sea capaz de resolver cualquiera de esos tres problemas y no sea capaz de resolver cualquiera de los otros, si carece de los esquemas operativos pertinentes, aunque tenga la capacidad de pensar hipotéticamente. Es decir, no hay razón para suponer que resolver exitosamente el problema de los líquidos va a permitir resolver exitosamente el problema de la balanza. En este sentido, ¿puede el ajedrez facilitar experiencias que ayuden a la adquisición de los esquemas lógicos subyacentes al problema de la balanza y al problema de los líquidos? La investigación de Johan Christiaen no encontró relación entre la instrucción en ajedrez y la prueba de la balanza, pero sí encontró alguna correlación positiva entre la instrucción en ajedrez y la resolución exitosa del test de los líquidos. En mi opinión, esta diferencia de resultados entre una y otra prueba tiene que ver con la específica naturaleza del pensamiento ajedrecístico.
La naturaleza lógica del ajedrez y el papel del pensamiento hipotético deductivo en el ajedrez.
El ajedrez no es un juego de matemáticas ni de lógica formal. Obsérvese que, aunque encontremos libros muy entretenidos sobre curiosidades matemáticas del ajedrez, serán muy pocos los artículos de ajedrez que resuelvan matemáticamente o lógicamente posiciones de ajedrez: básicamente, solo en determinados análisis de finales con muy pocas piezas, en los que predominarán temas como la oposición de reyes o el zugzwang, nos podremos encontrar con esquemas de Reciprocidad o de Correlación. Precisamente el encanto de los finales y por qué enamoran a cierto tipo de jugadores, reside en su naturaleza exacta, en tanto que el resto de fases del juego, singularmente la apertura y en gran medida también el medio juego, están caracterizados por la incertidumbre de las soluciones. La frase de Karpov “El ajedrez está más cerca de las Matemáticas que cualquier otra ciencia” es sencillamente falsa.
Lo que tienen en común los dos problemas de la balanza y los líquidos es que requieren para su resolución una exploración sistemática mediante operaciones mentales del espacio de lo posible. Y en ese sentido sí que, a ojos del lego, coinciden con el ajedrez. Esta era la hipótesis concreta de Johan Christiaen, que no tuvo en cuenta la distinta naturaleza de las operaciones en cada caso, por lo que no pudo prever que la correlación no fuera la misma con la prueba de la balanza que con el test de los líquidos.
 Ni el ajedrez es un juego de lógica, más que residualmente, ni tampoco es cierto que el ajedrez sea el territorio por excelencia del pensamiento hipotético deductivo. Ya desde el famoso artículo de Claude Shannon en 1949 (Programming a Computer for Playing Chess) quedó claro que el ajedrez es un juego irresoluble, incluso y todavía hoy para las máquinas. El único éxito de las computadoras en estos 80 años ha sido derrotar al ser humano, nada más y nada menos. Pero ninguna computadora ha presentado la partida perfecta, el juego perfecto que resuelve el problema del ajedrez: juegan blancas y…
Ni el ajedrez es un juego de lógica, más que residualmente, ni tampoco es cierto que el ajedrez sea el territorio por excelencia del pensamiento hipotético deductivo. Ya desde el famoso artículo de Claude Shannon en 1949 (Programming a Computer for Playing Chess) quedó claro que el ajedrez es un juego irresoluble, incluso y todavía hoy para las máquinas. El único éxito de las computadoras en estos 80 años ha sido derrotar al ser humano, nada más y nada menos. Pero ninguna computadora ha presentado la partida perfecta, el juego perfecto que resuelve el problema del ajedrez: juegan blancas y…
Para el ser humano, y también para la máquina todavía, el ajedrez es un juego de conjeturas, en feliz expresión creo que de Magnus Carlsen. En rigor, solo se podrían admitir como cálculo exacto, desde el punto de vista de agotar el juego, aquellas maniobras o tácticas que en una determinada posición llegan a una conclusión del juego forzada e irreversible: el mate o las tablas por ahogado o por insuficiencia de material. Es decir, muy pocas situaciones, y ni siquiera se dan en una mayoría de partidas no-tablas, en las que el perdedor resigna simplemente ¡por una conjetura que considera irrebatible!
Rebajando nuestra escala de rigor, podríamos aceptar también como “cálculo exacto” aquellas tácticas forzadas que producen un importante desequilibrio de material, del orden de una pieza menor o más. Son posiciones en las que un gran maestro o un jugador fuerte abandonará ante otro rival de fuerza similar, pero que un jugador de fuerza mediana quizás no pueda transformar en victoria frente a una computadora. A efectos prácticos, incluso podríamos añadir al “cálculo exacto” aquellas maniobras tácticas que consiguen de manera forzada un objetivo no resolutivo del juego, como una mejora posicional o una reubicación de piezas, sin entrar a valorar si la conjetura-guía, la supuesta mejora, es o no correcta: simplemente, uno de los jugadores ha conjeturado como beneficiosos un objetivo intermedio y se ha propuesto conseguirlo de una manera imposible de rebatir por su rival.
He subrayado la expresión “de manera forzada” en varias ocasiones porque muchas de las maniobras que se realizan en el transcurso de una partida, incluso algunas que ganan material o conducen al mate, no están apoyadas en un cálculo exacto sino en una conjetura o plausibilidad de réplicas del contrario. En ello tiene que ver en algunos casos la picardía del jugador, pero en otros muchos, la mayoría, que los patrones o esquemas de juego ocupan el lugar del razonamiento riguroso. Es decir, la Pericia.
En el ajedrez, la mayor oposición entre conjetura y cálculo exacto es la que se da entre la apertura y el final. El final es en gran medida el terreno de la comprensión lógica y del cálculo exacto. La apertura es por su naturaleza el terreno de la conjetura (centro, desarrollo, seguridad del rey, cosas así), que se apoya fortísimamente en la experiencia-expertise-pericia en el caso de jugadores avanzados, y en muchos otros casos en el triste aprendizaje memorístico. Si tuviéramos que enseñar ajedrez para preparar alumnos para superar pruebas de razonamiento hipotético deductivo, enseñaríamos finales, posiblemente táctica, pero nos saltaríamos las aperturas.
La incertidumbre del cálculo es el dominio de la pericia. Que las partidas blitz o bullet de los jugadores expertos sean de tan buena calidad que sirven de modelo a los jugadores que se inician, nos debería alertar de que el ajedrez no es tan exacto y sistemático como la fama que tiene. Y puede ser una explicación de por qué, en el estudio de Joahn Christiaen, ese año y medio de instrucción en ajedrez no produjo un mejor rendimiento en pruebas de razonamiento hipotético deductivo. Desconozco cómo fue la enseñanza impartida durante ese año y medio. No he podido localizar el Jeugd Schaak (Ajedrez para Jóvenes) de B. Withuis, pero el manual es holandés y hacia treinta años que el también holandés Adrian de Groot había publicado ya sus primeras investigaciones sobre el papel de los patrones visuales en ajedrez. Hoy es un lugar común enseñar patrones de todo tipo a los niños. Por ejemplo, se les presenta un motivo táctico como la descubierta y ese día y en días sucesivos realizan decenas de ejercicios sobre la descubierta. Desde un punto de vista deportivo, los resultados son muy rápidos, pero ¿qué ocurre con los procesos mentales? Si la pericia es la herramienta que nos permite dominar la incertidumbre, si los patrones nos permiten resolver situaciones tácticas casi sin pensar, ¿no es también un mal sustituto del esfuerzo mental, de ése “lo que se hace cuando no se sabe”, que es la definición de inteligencia?
Quizás ésta última reflexión no sea aplicable a un reducido número de adolescentes y jóvenes que destacan compitiendo duramente sobre los tableros reales, enfrentando continuamente el dilema de hasta cuándo y cuánto deben confiar en su intuición, en su pericia, y desde cuándo y cuánto deben entregarse al agónico cálculo exacto de variantes. Posiblemente éste es el auténtico campo de batalla del ajedrez, encontrar en cada momento el equilibrio justo entre la intuición (la pericia) y el cálculo exacto. ¿Pero podemos decir lo mismo de esa multitud de adictos al blitz que juegan miles de partidas al año en las plataformas online? El ajedrez, además de un paradigma de la mente cognitiva, es también una adicción. Pero ése es otro tema.
















